Proof of the abc Conjecture?
from Peter Woit’s blog “Not Even Wrong”
Proof of the abc Conjecture?
While I was traveling this past week, there was a conference held here entitled L-functions and Automorphic Forms, which was a celebration of the 60th birthday of my math department colleague Dorian Goldfeld. From all I’ve heard the conference was a great success, well attended, with lots of interesting talks. But by far the biggest excitement was due to one talk in particular, that of Lucien Szpiro on “Finiteness Theorems for Dynamical Systems”. Szpiro, a French mathematician who often used to be a visitor at Columbia, but is now permanently at the CUNY Graduate Center, claimed in his talk to have a proof of the abc conjecture (although I gather that, due to Szpiro’s low-key presentation, not everyone in the audience realized this…).
The abc conjecture is one of the most famous open problems in number theory. There are various slightly different versions, here’s one:
For each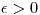 
0" alt="\epsilon >0" align="absmiddle"> there exists a constant 
such that, given any three positive co-prime integers 
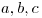satisfying 
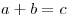, one has
where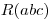 
is the product of all the primes that occur in 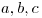, each counted only once.
The abc conjecture has a huge number of implications, including Fermat’s Last Theorem, as well as many important open questions in number theory. Before the proof by Wiles, probably quite a few people thought that when and if Fermat was proved it would be proved by first proving abc. For a very detailed web-site with information about the conjecture (which leads off with a quotation from Dorian “The abc conjecture is the most important unsolved problem in diophantine analysis”), see here. There are lots of expository articles about the subject at various levels, for two by Dorian, see here (elementary) and here (advanced).
As far as I know, Szpiro does not yet have a manuscript with the details of the proof yet ready for distribution. Since I wasn’t at the talk I can only relay some fragmentary reports from people who were there. Szpiro has been teaching a course last semester which dealt a bit with the techniques he has been working with, here’s the syllabus which includes:
We will then introduced the canonical height associated to a dynamical system on the Riemann Sphere. We will study such dynamical systems from an algebraic point of view. In particular we will look at the dynamics associated to the multiplication by 2 in an elliptic curve . We will relate these notions and the questions they raised to the abc conjecture and the Lehmer conjecture.
For more about these techniques, one could consult some of Szpiro’s recent papers, available on his web-site.
The idea of his proof seems to be to use a and b to construct an elliptic curve E, then show that if abc is wrong you get an E with too many torsion points over quadratic extensions of the rational numbers. The way he gets a bound on the torsion is by studying the “algebraic dynamics” given by the iterated map on the sphere coming from multiplication by 2 on the elliptic curve. I’m not clear about this, but it also seems that what Szpiro was proving was not quite the same thing as abc (his exponent was larger than 
, something which doesn’t change many of the important implications).
Maybe someone else who was there can explain the details of the proof. I suspect that quite a few experts are now looking carefully at Szpiro’s arguments, and whether or not he actually has a convincing proof will become clear soon.
7 Responses to “Proof of the abc Conjecture?”
posted by Wang Yonghui @ 10:05 AM
May 26th, 2007 at 8:07 pm
This would be most remarkable and exciting if true! I seem to recall that the good professor Terry Tao mentions the opinion of another mathematician, Shou Wu Zhang, on how the abc conjecture could be proved, namely, saying that it would follow if one assumed enough variants of the BSD and RH conjectures.
http://terrytao.wordpress.com/2007/05/04/distinguished-lecture-series-iii-shou-wu-zhang-“triple-l-series-and-effective-mordell-conjecture”/
So if abc is true, while it is obviously not strong enough to provide any information about these other extremely famous conjectures, the remark of Shou Wu Zhang seems to indicate that at least it doesn’t rule them out (in their full generality) by contradiction.
May 27th, 2007 at 8:03 am
I’m told by a mathematician friend that abc doesn’t imply Fermat; it implies asymptotic Fermat (sufficiently large exponents).
May 27th, 2007 at 8:42 am
I agree with David S-D…in particular, on the site about the ABC conjecture which you link to, the consequence is said to be:
“that there are only finitely many solutions to the equation x^n+y^n=z^n with gcd(x,y,z)=1 and n> 3.”
May 27th, 2007 at 9:17 am
I should have been more precise. It’s true that abc only implies Fermat for big enough n, but Fermat is known to be true by other methods for a large range of n, so abc would finish the proof (without Taylor-Wiles). You do have to check the coefficient you get in abc to make sure the ranges overlap, they do for Szpiro’s proof.
May 27th, 2007 at 11:02 pm
Peter,
The way you phrase the abc-conj above, it appears that C_\epsilon depends on a, b and c. The way I would phrase it would be to say,
that given any epsilon > 0, there exists a constant C_\epsilon
such that for any triple of positive integers a, b, c with a+b = c and gcd(a,b,c) =1… [etc]. Agree?
-Kasper
May 29th, 2007 at 10:19 am
Kasper,
Yes, that’s right, I should have written things in another order to make that clear. The constant doesn’t depend on a,b,c. Maybe I’ll change it now…
May 29th, 2007 at 4:38 pm
According to Wikipedia http://organizationsandmarkets.com/
Szpiro announced a proof of the ‘Weak abc conjecture’. The paper http://www.math.columbia.edu/~goldfeld/ABC-Conjecture.pdf mentions a ‘weak abc conjecture’.